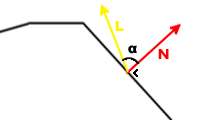
Light and normal vectors
To overcome some of the limitations of the ambient lighting model we will now add a diffuse
lighting term to the shader. The diffuse lighting model will take the light direction and the
surface orientation into account to calculate the amount of light that is reflected from the
surface into all directions. Because the light is reflected equally into all directions the diffuse
lighting is not dependent on the view position. This makes it suitable for simulating matte
surfaces like paper.
Diffuse light is emitted by dynamic light sources and by the sun. From now on, L is the light direction vector and N is the surface normal:

Light and normal vectors
The amount of light that is reflected is directly proportional to the angle between the light
direction and the surface normal. When N and L are aligned (in other words: when the light
beam is perpendicular to the surface) the reflection is at its peak, when N and L are
perpendicular, no diffuse light is reflected.
If we take the cosine of the angle between N and L we get 1 when they are aligned and 0
when they are perpendicular. We don't know the angle between N and L, but we can use the
following property of the dot product to calculate it:
N · L = |N| * |L| * cos(α)
|N| is the magnitude of the vector N. If we use normalized vectors we can simplify this to:
N · L = 1 * 1 * cos(α) = cos(α)
The dot product equals cos(α) if N and L are unit vectors. The diffuse equation is:
Diffuse Light = Diffuse Intensity * N · L
Our entire equation is now:
Final Color = (Diffuse Light + Ambient Light) * Diffuse Color
The diffuse color will be read from the texture map.
// Tweakables:
static const float AmbientIntensity = 1.0f; // The intensity of the ambient light.
static const float DiffuseIntensity = 1.0f; // The intensity of the diffuse light.
static const float4 SunColor = {0.9f, 0.9f, 0.5f, 1.0f}; // Color vector of the sunlight.
// Application fed data:
const float4x4 matWorldViewProj; // World*view*projection matrix.
const float4x4 matWorld; // World matrix.
const float4 vecAmbient; // Ambient color, passed by the engine.
const float4 vecSunDir; // The sun direction vector.
texture entSkin1; // Model texture
// Color map sampler
sampler ColorMapSampler = sampler_state
{
Texture = <entSkin1>;
AddressU = Clamp;
AddressV = Clamp;
};
// Vertex Shader:
void DiffuseVS(
in float4 InPos: POSITION,
in float3 InNormal: NORMAL,
in float2 InTex: TEXCOORD0,
out float4 OutPos: POSITION,
out float2 OutTex: TEXCOORD0,
out float3 OutNormal: TEXCOORD1)
{
// Transform the vertex from object space to clip space:
OutPos = mul(InPos, matWorldViewProj);
// Transform the normal from object space to world space:
OutNormal = normalize(mul(InNormal, matWorld));
// Pass the texture coordinate to the pixel shader:
OutTex = InTex;
}
// Pixel Shader:
float4 DiffusePS(
in float2 InTex: TEXCOORD0,
in float3 InNormal: TEXCOORD1): COLOR
{
// Calculate the ambient term:
float4 Ambient = AmbientIntensity * vecAmbient;
// Calculate the diffuse term:
float4 Diffuse = DiffuseIntensity * SunColor * saturate(dot(-vecSunDir, normalize(InNormal)));
// Fetch the pixel color from the color map:
float4 Color = tex2D(ColorMapSampler, InTex);
// Calculate final color:
return (Ambient + Diffuse) * Color;
}
// Technique:
technique DiffuseTechnique
{
pass P0
{
VertexShader = compile vs_2_0 DiffuseVS();
PixelShader = compile ps_2_0 DiffusePS();
}
}
We will first take a look at the variable definitions because some have been added:
// Tweakables:
static const float AmbientIntensity = 1.0f; // The intensity of the ambient light.
static const float DiffuseIntensity = 1.0f; // The intensity of the diffuse light.
static const float4 SunColor = {0.9f, 0.9f, 0.5f, 1.0f}; // Color vector of the sunlight.
// Application fed data:
const float4x4 matWorldViewProj; // World*view*projection matrix.
const float4x4 matWorld; // World matrix.
const float4 vecAmbient; // Ambient color, passed by the engine.
const float4 vecSunDir; // The sun light direction vector.
texture entSkin1; // Model texture
// Color map sampler
sampler ColorMapSampler = sampler_state
{
Texture = <entSkin1>;
MipFilter = Linear; // required for mipmapping
AddressU = Clamp;
AddressV = Clamp;
};
As you can see, two new variables have been added under tweakables. One is the diffuse
intensity and the other is the color of the sunlight (feel free to experiment with different
intensity and color values!). Next we define a second matrix for transforming the vertex normal from object space to world
space. We have also added a new vector that will be set to the sun light direction by the engine.
Next we define a texture. The texture is also sent from the engine and thus must be named
according to the list of effect variables from the manual: entSkin1 for the first model skin.
This shader will expect that the color texture is stored in entSkin1 that was set up in MED.
Next we define a sampler. A sampler is an object that defines how a texture should be read.
All we specify for this sampler, called ColorMapSampler is that if the texture coordinates are
outside the texture size, they are Clamped - the last pixel of the texture is returned. We could also omit the AddressU/AddressV lines or choose to Wrap the coordinates (which is the default) for repeating textures. We also specify a linear mipmap filter - by default, sampers don't support mipmapping. For a full list of sampler_state settings,
check MSDN (see Further Reading section of this tutorial).
The vertex shader for our diffuse lighting tutorial is only slightly more complex than that of
the ambient lighting shader:
// Vertex Shader:
void DiffuseVS(
in float4 InPos: POSITION,
in float3 InNormal: NORMAL,
in float2 InTex: TEXCOORD0,
out float4 OutPos: POSITION,
out float2 OutTex: TEXCOORD0,
out float3 OutNormal: TEXCOORD1)
{
// Transform the vertex from object space to clip space:
OutPos = mul(InPos, matWorldViewProj);
// Transform the normal from object space to world space:
OutNormal = normalize(mul(InNormal, matWorld));
// Pass the texture coordinate to the pixel shader:
OutTex = InTex;
}
We define the function DiffuseVS which takes three input vectors and also returns three vectors. The input vectors are automatically set to the POSITION, NORMAL and first texture coordinate (TEXCOORD0) of the vertex by DirectX (which in turn receives it from the engine, see chapter: "D3D Pipeline") because they are marked with the corresponding input semantic.
We need three output vectors, so we can't return them directly (except if we had defined a struct for them). Thus we're putting them marked as out in the function argument list. You might wonder why we've used the TEXCOORD1 rather than the NORMAL semantic for the output OutNormal vector. The reason is that we want to pass this vector to the pixel shader function which accepts TEXCOORDs, but no POSITION and no NORMAL.
In the vertex shader we once again transform the position. After that, the normal is transformed to
world space. Since vecSunDir is already in world space, the vertex normal must also be in world
space in order to compare it to the sun direction vector in the pixel shader. We then proceed to
pass the input texture coordinates to the output variables. We don't need to change the texture
coordinate for this shader.
Almost the whole theory we have discussed is executed in the pixelshader:
// Pixel Shader:
float4 DiffusePS(
in float2 InTex: TEXCOORD0,
in float3 InNormal: TEXCOORD1): COLOR
{
// Calculate the ambient term:
float4 Ambient = AmbientIntensity * vecAmbient;
// Calculate the diffuse term:
float4 Diffuse = DiffuseIntensity * SunColor * saturate(dot(-vecSunDir, normalize(InNormal)));
// Fetch the pixel color from the color map:
float4 Color = tex2D(ColorMapSampler, InTex);
// Calculate final color:
return (Ambient + Diffuse) * Color;
}
First we define the function DiffusePS which takes two vectors as input and returns a color vector. Remember we marked the output variables of the vertex shader with TEXCOORD0 and TEXCOORD1? The data that we put in it in the vertex shader (a texture coordinate and a
normal) has now been interpolated between the three vertices that form the triangle on which this
pixel is situated. The interpolated result is put back in the TEXCOORD0 and TEXCOORD1
registers. So now that we have a texture coordinate that is somewhere in between the texture
coordinates of the three vertices forming the triangle this pixel is on, we can use it to do a
lookup from the texture.
First we calculate the ambient component just like in the last chapter. Only this time, we store
it in a new vector called "Ambient" that we can use later on to calculate the final color.
We then continue by calculating the diffuse component. Remember the formula?
Here it is again:
Diffuse Light = Diffuse Intensity * N · L
Let's take the next line apart.
float4 Diffuse = DiffuseIntensity * SunColor * saturate(dot(-vecSunDir, normalize(InNormal)));
First we normalize the vector InNormal. This is necessary because it may have been "denormalized" by the interpolation between the triangle vertices. If you use a non normalized vector to calculate the dot product the result will be different because the following rule would not apply anymore:
N · L = |N| * |L| * cos(α) = 1 * 1 * cos(α) = cos(α)
So we take the dot product of the sun direction (which was passed by the engine) and the
normalized vertex normal. We use the negative of the sun light direction because we need a vector pointing towards the sun, not away from it. Both are unit vectors, so the result of the dot product is the
cosine of the angle between those vectors.
We then use the saturate intrinsic function to clamp the value of the dot product between 0
and 1. We don't want to assign `negative light' to surfaces that are facing away from the light!
Next we multiply the calculated value by the color of the sunlight. What happens here is that
the R, G and B components of the original color get increased or decreased individually,
making the resulting color more red, green or blue depending on the SunColor RGB values.
We then read the color from the color map. We use the tex2D intrinsic function to read a color vector from the ColorMapSampler at the coordinates given by InTex. Finally, we return the total amount of light (Ambient + Diffuse), multiplied with the color from the texture map.
Open diffusedemo.c in SED and run it:

We can now see the surface of the object and we can tell where the light is coming from. We can also see the texture that we have assigned to the model. Note that we've added some lines of code that lets the sun orbit around the object. However, the lighting is independent of the viewers' position. This is ok for matte surfaces, but polished, shiny surfaces do not reflect light equally into every direction. In our next workshop we will enhance the lighting algorithm to make it suitable for shiny surfaces.