
In this section I will provide an overview of the mathematical concepts behind many graphics algorithms. I will not go into too much detail because this is an entry level tutorial. If you would like get a more in-depth understanding of the mathematics, please see the further reading section.
For the mathematicians out there, please note that I will sometimes present concepts in a simplified way to make it easier to understand for newbies at the cost of completeness and correctness. For example, I will not explain that a vectors' properties are independent from
the coordinate system it is represented in because we only use the Cartesian system.
A vector is characterized by a magnitude (length) and a direction. A vector consists of several numbers and is defined like this:
V = [e1, e2, e3, ..., en]
It is best to imagine a vector as an arrow, see figure below. As a programmer, you can also imagine a vector as an array of numbers.

Graphical representation of a few 2D vectors.
A = [2, 2]
B = [1, -3]
C = [2, 2]
Note that vector A and vector C are the same because they have the same magnitude and direction. A vector is NOT defined by its starting point; in fact it doesn't have one.
The number of elements of a vector are also known as its dimension. A vector can have any dimension but in graphics programming we mostly use 3D and 4D vectors. For the following
examples however, I will mostly use 2D vectors because they are easier to visualize.
The vector as described above is a spatial vector. Vectors are also used to store colors (red,
green, blue, alpha) or positions (which are basically direction vectors that start at the origin).
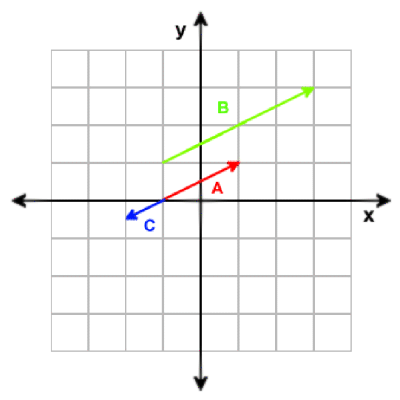
Addition of vectors is done by adding the corresponding components of each vector. Example:
A = [3, 1]
B = [0, 2]
A + B = [3 + 0, 1 + 2] = [3, 3]
 Wii Dev Kit
Wii Dev Kit
Adding two vectors results in a third vector encompassing both displacements.
Subtraction of vectors is done by subtracting the corresponding components of each vector. Example:
A = [-3, 2]
B = [2, 3]
A B = [(-3) - 2, 2 - 3)] = [-5, -1]
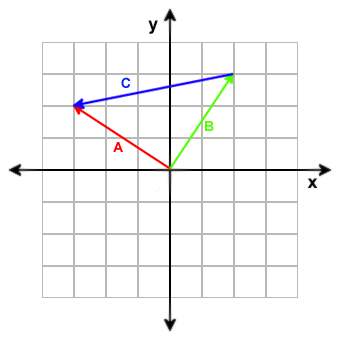
Subtracting two vectors results in a third vector pointing from the end point of the second
vector to the end point of the first vector. It is often used in shaders for getting a direction vector between two points.
Multiplication of two vectors is done by multiplying the corresponding components. Example:
A = [3, 5, 1]
B = [2, 2, 3]
A * B = [3 * 2, 5 * 2, 1 * 3] = [6, 10, 3]
Multiplying two vectors is rarely used in vector math, but you'll find very often the multiplication of a vector with a matrix, which we'll deal with later.
The magnitude, or length of a vector is denoted by two vertical stripes on either side of the vector: |V|. It can be calculated with Pythagoras' theorem. For those of you that don't know or forgot it:
|V| = square-root ((Vx)2 + (Vy)2 + (Vz)2)
Scaling a vector is done by multiplying each component with a scalar (a number). If the scalar is negative, the direction of the vector is also inverted. Example:
A = [2, 1]
B = 2 * A = [4, 2]
C = -0.5 * A = [-1, -0.5]
Multiplying a vector with a scalar will only change the magnitude of the vector. If the scalar
is negative, the vector is also inverted.
A unit vector is any vector of length one. This does not mean that all components must be 1. Example:
A = [1, 1]
B = [0.71, 0.71]
C = [1, 0]
|A| = square-root(12 + 12) = 1.41, so
A is NOT a unit vector.
|B| = square-root(0.712, 0.712) = 1, so
B is a unit vector.
|C| = square-root(12, 02) = 1, so C is a unit vector.
For many calculations in lighting algorithms the vectors must be unit vectors. You can convert an arbitrary vector to a unit vector, this is called normalization. To normalize a vector
you must divide each component of the vector by its length.
Example:
V = [4, 4]
|V| = square-root(42 + 42) = square-root(32) = 5.66
Vnormalized = [4 / 5.66, 4 / 5.66] = [0.71, 0.71]
And to prove that it's actually normalized:
| Vnormalized | = square-root(0.712 + 0.712) = 1
The dot product is a very important operation in graphics programming. The interesting thing about it is that the result is not a vector but a single number (a scalar). It can be used to find the angle between two vectors. The dot product is defined as:
A · B = |A| * |B| * cos(A,B)
The dot product is the length of vector A, multiplied by the length of vector B, multiplied by
the cosine of the angle between A and B. Because in shader programming we usually don't know the angle between A and B, this is of little use to us. Fortunately, there is another way to
calculate the dot product:
A · B = Ax * Bx + Ay * By + Az * Bz
The dot product is the same as the sum of all vector components multiplied with each other. To find the angle between A and B, we simply divide this value by the product of |A| and |B|. In the case of normalized vectors the dot product is equal to the cosine of the angle between A and B because |A| and |B| are both 1.
The cross product of two vectors is a vector that is perpendicular to both. It is defined as:
A x B = |A| * |B| * sin(A,B) * N
where N is the unit vector perpendicular to A and B. We usually don't know the angle between A and B, but again there is another way to calculate the cross product:
A x B = [Ay * Bz - Az * By, Az * Bx - Ax * Bz, Ax * Cy - By * Bz]
In shaders, the cross product is usually used to find the third axis vector of a coordinate system when the two other vectors are known. The order of components to multiply and subtract can be memorized by the "xyzzy" rule (x component of the result = Ay * Bz - Az * By).
Another important concept to grasp is coordinate spaces. You will be dealing with it in pretty
much every shader you will write. You've probably already used them without even knowing
it.
In computer graphics we use the 3D Cartesian coordinate system to represent vectors. This
means that a vector is represented by an x, y and z coordinate that give the displacement from
the origin in the direction of an axis. But what does it mean when an object is at a certain
point on an axis? Where is the origin and in what directions do the axes go? What values may
be used to define a vector? The answers to those questions are different in different coordinate spaces.
The first thing you have to keep in mind is that the level coordinate system is not the same as the DirectX coordinate system. When editing a level, model, or terrain in Gamestudio, you're using level coordinates with an XY grid for the level map and height given by Z axis. DirectX however uses a different coordinate system with an XZ grid for the level map and the height given by the Y axis. There is no mathematical reason for having those two different coordinate systems - it's just tradition. Anyway when dealing with shaders, you're using DirectX coordinates. Thus they are automatically converted from level coodinates when they are passed to the shader. But this is only the first step in coordinate conversion. There are five more coordinate systems used in shader programming: the texture space, the object space, the world space, the camera space, and the clip space.
Texture space - sometimes called tangent space - is the coordinate space of texture coordinates. Although texture coordinates are usually 2 dimensional, texture space is 3 dimensional for easier transforming 3D positions and directions to it. The coordinate axes of texture space run along the u and v coordinates of the texture, parallel to the surface; the third axis runs along the surface normal vector that is perpendicular to the surface. Because a surface usually is not flat but bent in 3D space, texture space is different at every position of the surface.
Object space - sometimes called local space - is the coordinate space in which vertex positions are stored. The origin or null
vector (0,0,0) is at the origin of the model (which is the (x,y,z) position of the object in the
world) and its axes go from left to right, from down to up and from the back to the front of the
model. If you move or rotate an object in the world, the vertex positions in object space will
not change, only the origin or axes of the object in the world change but the vertices are at the
still position on those axes.
Object positions are usually stored in world space. The world space origin and axes are those
that you see when you create a level in Gamestudios' World Editor (WED). They are not
defined by anything else.
Gamestudio's "view entities" are in camera space (sometimes called view space). This means that the origin is at the
camera and the axes point up/down, right/left and into your monitor.
Lastly there is clip space. In clip space, all coordinates range from [-1..1] on all axes. In clip
space, only the objects that are visible (the objects that are within the viewing volume) are
present and far away objects are smaller than close-by objects. Clip space is the perspective transformed camera space, and is used for finally drawing the actual objects on the screen.
A matrix is a two dimensional grid of values. It's basically a row (or column) of vectors. A matrix is usually represented by a multidimensional array in code. Example:
1, 0, 0
2, 0, 0
0, 3, 0
This is a 3x3 matrix M with:
M[0, 0] = 1
M[1, 0] = 2
M[2, 1] = 3
All other values of M are at 0.
By multiplying all vertices of an object with a matrix it is possible to move, rotate and scale objects, and transform position vectors into different coordinate spaces. All those operations are called transformations. When multiplying two matrices the resulting matrix will encompass both transformations.
For more information on matrices, see the "Further Reading" section.