Vektor-Berechnungen

Die Vektor-Funktionen arbeiten mit dreidimensionalen Vektoren, d. h. mit Gruppen von 3 Zahlen (s.u.). Vekroren werden für unterschiedliche Zwecke verwendet, meist zum Beschreiben einer x-, y-, z-Position, einer Richtung oder Geschwindigkeit, sowie einer Blau-Grün-Rot-Farbe (blue green red) oder einem pan tilt roll-dreidimensionalen Euler-Winkel.

Jeder var-Array der Länge 3, sowie jedwede drei aufeinanderfolgenden Skills oder var-Parameter eines Objektes lassen sich als Vektor verwenden. Um beispielsweise die x-, y-, z-Parameter der my-Entity als Positions-Vektor zu verwenden, übergeben Sie der Vektor-Funktion einfach my.x. Gültige Vektor-Parameter sind demnach

jedwedes vordefinierte VECTOR-, ANGLE-, or COLOR-Stukt und jede Variable, die als var[3] definiert ist;
jedes Element eines Variablen-Arrays, das mindestens 3 weniger als die Länge des Arrays ist (etwa array[0], array[3], array[6]...);
jeder Entity-Skill zwischen skill1 undskill96;
die x-, pan-, oder blue-Parameter jedweder Entity, eines jeden Partikels oder Views.

Wird dann, wenn ein Vektor erwartet wird, irgend etwas anderes gegeben, kann dies einen Engine-Absturz zur Folge haben - die Gültigkeit von Vektoren wird aus Geschwindigkeitsgründen nicht geprüft.

Was ist ein Vektor?

Ein Vektor wird durch eine Größe (Länge) und eine Richtung charakterisiert. Ein Vektor besteht aus mehreren Zahlen und wird wie folgt definiert:

V = [e1, e2, e3, ..., en]

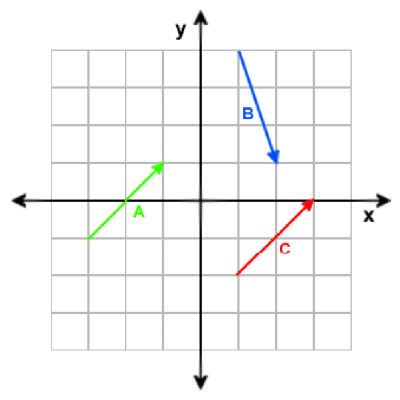
Am Besten stellt man sich einen Vektoren als einen Pfeil vor, siehe Figur unten. Als Programmierer können Sie sich einen Vektoren auch als einen aus Zahlen bestehenden Array vorstellen.

Graphische Darstellung von ein paar 2D-Vektoren.

A = [2, 2]
B = [1, -3]
C = [2, 2]

Beachten Sie, daß Vektor A und Vektor C dasselbe sind, denn sie haben dieselbe Größe und Richtung. Ein Vektor wird NICHT durch seinen Startpunkt definiert, in Wahrheit hat er gar keinen.

Die Anzahl der Elemente eines Vektors kennt man auch als seine Dimension. Ein Vektor kann jedwede Dimension haben, in der Graphik-Programmierung verwenden wir aber meist 3D- und 4D-Vektoren. Für die folgenden Beispiele jedoch, werde ich meist 2D-Vektoren verwenden, denn die sich vorzustellen, ist einfacher.

Der oben beschriebene Vektor ist ein Räumlicher. Vektoren werden auch zum Speichern von Farben (Rot, Grün, Blau), Winkel (pan, tilt, roll) oder Positionen (die im Grunde Richtungsvektoren sind, welche im Ursprung starten) verwendet.

Vektor-Addition

Das Addieren von Vektoren geschieht durch Addieren der entsprechenden Komponenten eines jeden Vektors. Beispiel:

A = [3, 1]
B = [0, 2]
A + B = [3 + 0, 1 + 2] = [3, 3]

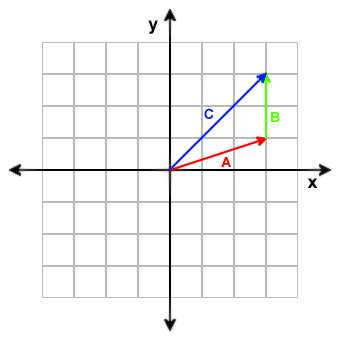
Das Addieren zweier Vektoren resultiert in einem dritten Vektor, der beide Verschiebungen einschließt.

Vektor-Subtraktion

Das Substrahieren von Vektoren geschieht durch Substrahieren der entsprechenden Komponenten eines jeden Vektors. Beispiel:

A = [-3, 2]
B = [2, 3]
A B = [(-3) - 2, 2 - 3)] = [-5, -1]

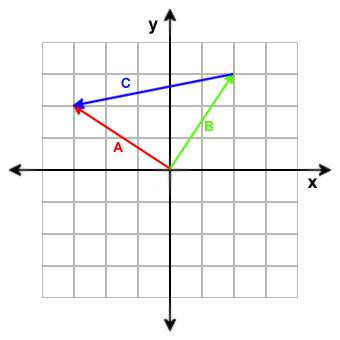
Das Substrahieren zweier Vektoren resultiert in einem dritten Vektor, der vom Endpunkt des zweiten Vektoren zum Entpunkt des ersten Vektoren zeigt. Das wird oft in Shadern verwendet, um einen Richtungsvektoren zwischen zwei Punkten zu erhalten.

Vektor-Multiplikation

Das Multiplizieren zweier Vektoren geschieht durch Multiplizieren der betreffenden Komponenten. Beispiel:

A = [3, 5, 1]
B = [2, 2, 3]
A * B = [3 * 2, 5 * 2, 1 * 3] = [6, 10, 3]

Die Multiplikation zweier Vektoren wird in der Vektoren-Mathematik selten benutzt, ziemlich oft finden Sie aber die Multiplikation eines Vektors mit einer Matrix womit wir uns später befassen.

Größe eines Vektors

Die Größe oder Länge eines Vektors ist durch zweit vertikale Streifen an jeder Seite des Vektors gekennzeichnet: |V|. Sie kann mit dem Satz des Pythagoras berechnet werden. Für diejenigen unter Ihnen, die ihn nicht kennen oder vergessen haben:

|V| = square-root ((Vx)² + (Vy)² + (Vz)²)

Ein Vektor des Umfanges 1 wird Einheitsvektor (unit vector) genannt (s. unten).

Skalieren eines Vektors

Das Skalieren eines Vektors geschieht durch Multiplizieren jeder Komponente mit einem Skalar (einer Zahl). Ist der Skalar negativ, wird auch die Richtung des Vektoren umgekehrt. Beispiel:

A = [2, 1]
B = 2 * A = [4, 2]
C = -0.5 * A = [-1, -0.5]

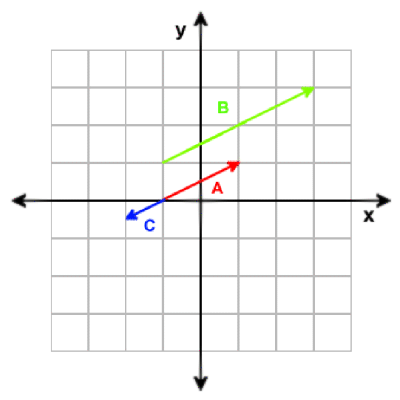
Das Multiplizieren eines Vektoren mit einem Skalar ändert nur die Größe des Vektors. Ist der Skalar negativ, wird auch der Vektor umgekehrt.

Einheitsvektoren

Ein Einheitsvektor ist jeder Vektor der Länge Eins. Dies bedeutet nicht, dass alle Komponenten 1 sein müssen. Beispiel:

A = [1, 1]
B = [0.71, 0.71]
C = [1, 0]

|A| = square-root(1² + 1²) = 1.41, A ist somit KEIN Einheitsvektor.
|B| = square-root(0.71², 0.71²) = 1, B ist also ein Einheitsvektor.
|C| = square-root(1², 0²) = 1, C ist somit ein Einheitsvektor.

Für viele Berechnungen in Beleuchtungsalgorithmen müssen die Vektoren Einheitsvektoren sein. Normale beispielsweise - die seknrecht zu einer bestimmten Oberfläche stehen - sind immer Einheitsvektoren. Sie können einen beliebigen Vektoren in einen Einheitsvektor konvertieren, das nennt man dann Normalisierung. Um einen Vektoren zu normalisieren, müssen Sie jede Komponente des Vektoren durch seine Länge dividieren. Beispiel:

V = [4, 4]
|V| = square-root(4² + 4²) = square-root(32) = 5.66
Vnormalized = [4 / 5.66, 4 / 5.66] = [0.71, 0.71]

And to prove that it's actually normalized:

| Vnormalized | = square-root(0.712 + 0.712) = 1

Punktprodukt

Das Punktprodukt ist beim Graphik-Programmieren eine sehr wichtige Operation. Das Interessante daran ist, daß das Ergebnis kein Vektor sondern eine einzelne Zahl (ein Skalar) ist. Es läßt sich zum Finden des Winkels zwischen zwei Vektoren verwenden. Das Punktprodukt wird definiert als:

A · B = |A| * |B| * cos(A,B)

Das Punktprodukt ist die Länge von Vektor A multipliziert mit der Länge von Vektor B, multipliziert mit dem Cosinus des Winkels zwischen A und B. Da wir beim Shader-Programmieren für gewöhnlich den Winkel zwischen A und B nicht kennen, ist dies für uns von wenig Nutzen. Glücklicherweise gibt es einen anderen Weg, das Punktprodukt zu berechnen:

A · B = Ax * Bx + Ay * By + Az * Bz

Das Punktprodukt ist dasselbe wie die Summe sämtlicher miteinander multiplizierter Vektorenkomponenten. Um den Winkel zwischen A und B herauszufinden, dividieren wir diesen Wert einfach durch das Produkt von |A| und |B|. Im Falle von normalisierten Vektoren ist das Punktprodukt gleich dem Cosinus des Winkels zwischen A und B, denn |A| und|B| sind beide 1.

Kreuzprodukt

Das Kreuzprodukt zweier Vektoren ist ein Vektor, der senkrecht zu beiden steht. Er wird definiert als:

A x B = |A| * |B| * sin(A,B) * N

wo N der Einheitsvektor und senkrecht zu A und B ist. Wir wissen für gewöhnlich den Winkel zwischen A und B nicht, aber wieder gibt es einen anderen Weg, auch das Kreuzprodukt zu berechnen.

A x B = [Ay * Bz - Az * By, Az * Bx - Ax * Bz, Ax * Cy - By * Bz]

In Shadern wird das Kreuzprodukt normalerweise zum Finden des Vektoren der dritten Achse eines Koordinatensystems benutzt, wenn die beiden anderen Vektoren bekannt sind. Die Reihenfolge der zu multiplizierenden und abzuziehenden Komponenten läßt sich durch die Regel "xyzzy" merken (x Komponente des Ergebnisses = Ay * Bz - Az * By).

(Einweisung und Bilder aus dem Shader-Workshop von Taco Cohen)

► Aktuelle Version Online