Trigonometrie-Einführung
Die folgende Einführung behandelt Winkel und trigonometrische Funktionen. Es gibt 6 grundlegende trigonometrische Funktionen, die am einfachsten an Hand eines rechtwinkligen Dreiecks erklärt werden können. In diesem Dreieck gibt es einen unbekannten Winkel x, wie in der abgebildeten Zeichnung.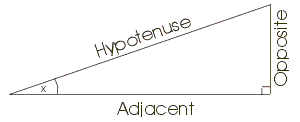
Die grundlegenden Funktionen verwenden für die Berechnungen die Längen der Hypothenuse (die längste Seite), der Gegenkathede (Opposite), die dem Winkel x gegenübersteht, und die Ankathete (Adjacent), die am Winkel x anliegt.
Der Sinus von x, geschrieben sin(x), ist definiert als:
| sin (x) | = | Gegenkathete |
| Hypothenuse |
Der Cosinus von x, geschrieben cos(x), ist definiert als:
| cos (x) | = | Ankathete |
| Hypothenuse |
Der Tangens von x, geschrieben tan(x), ist definiert als:
| tan (x) | = | Gegenkathete |
| Ankathete |
Beachten Sie, dass tan(x) an der Stelle x = 0 undefiniert ist.
Wenn ein Winkel und die Länge einer Seite eines rechtwinkligen Dreiecks bekannt sind, kann die zweite Seite sehr einfach ermittelt werden.
| Für Winkel zwischen 90 und 180 Grad: sin(x) == sin(180 - x) cos(x) == - cos(180 - x) tan(x) == - tan(180 - x) |
Für Winkel zwischen 0 bis 90 Grad: |
| Für Winkel zwischen 180 und 270Grad: sin(x) == - sin(180 + x) cos(x) == cos(180 + x) tan(x) == - tan(180 + x) |
Für Winkel zwischen 270 und 360 Grad: sin(x) == - sin(360-x) cos(x) == - cos(360-x) tan(x) == tan(360-x) |
Sin-1(x) bzw. asin(x) bezeichnet die inverse Sinusfunktion oder Arcus Sinus. Diese gibt den Winkel an, dessen SInus x ist. Ähnlich auch Arcus Cosinus und Arcus Tangens. Ein kurzer Blick auf die obige Tabelle zeigt, dass es für eine Arcusfunktion verschiedene Antworten geben kann. Deswegen benötigen physikalische Formeln mit Arcusfunktionen in der Regel den Bereich, in dem der Winkel liegen darf.
Bemerkungen:
Von C-Skript werden trigonometrische Funktionen für var-Variablen unsterstützt, von lite-C für var (im Pure-Modus) und für double. Die var-Funktionen verwenden aus Kompatibilitätsgründen mit Gamestudio Winkel in Grad (0...360), ihre Gegenstücke, double, hingegen verwenden Winkel in Radianten (0...2 pi), um mit C kompatibel zu sein. Seien Sie sich also immer im Klaren darüber, welchen Winkelbegriff Sie verwenden wollen!|
|
Einige nützliche Funktionen:
|
tan(x) = sin(x) / cos(x) |
|
sin(x-y) = sin(x) cos(y) - cos(x) sin(y) |
|
cos(x+y) = cos(x) cos(y) - sin(x) sin(y) |
|
cos(x-y) = cos(x) cos(y) + sin(x) sin(y) |
|
tan(x+y) = (tan(x) + tan(y)) / (1 - tan(x) tan(y)) |
|
tan(x-y) = (tan(x) - tan(y)) / (1 + tan(x) tan(y)) |
Indem wir in den obigen Formeln x = y ersetzen, erhalten wir:
|
sin(2x) = 2 sin(x) cos(x) |
|
cos(2x) = cos2(x) - sin2(x) |
|
tan(2x) = 2 tan(x) / (1 - tan2(x)) |