The vector functions operate on three-dimensional vectors, i.e. groups of three numbers (see below). Vectors are used for different purposes, mostly for describing a x y z position, a direction or speed, or a blue green red color , or a pan tilt roll 3-dimensional Euler angle.
Any var array of length 3, or any three consecutive skills or var parameters of an object can be used as a vector. For instance, to use the my entities' x y z parameters as a position vector, just pass my.x to the vector function. Thus, valid vector parameters are
If anything else is given when a vector is expected, an engine crash can be the result - the validity of vectors is not checked for speed reasons.
A vector is characterized by a magnitude (length) and a direction. A vector consists of several numbers and is defined like this:
V = [e1, e2, e3, ..., en]
It is best to imagine a vector as an arrow, see figure below. As a programmer, you can also imagine a vector as an array of numbers.

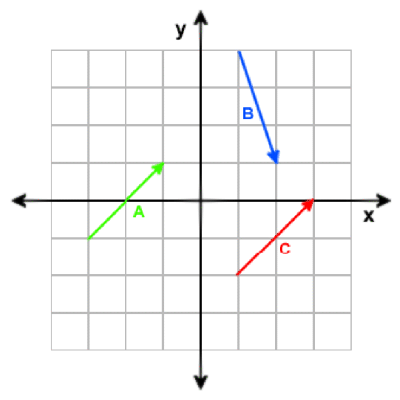
Graphical representation of a few 2D vectors.
A = [2, 2]
B = [1, -3]
C = [2, 2]
Note that vector A and vector C are the same because they have the same magnitude and direction. A vector is NOT defined by its starting point; in fact it doesn't have one.
The number of elements of a vector are also known as its dimension. A vector can have any dimension but in graphics programming we mostly use 3D and 4D vectors. For the following examples however, I will mostly use 2D vectors because they are easier to visualize.
The vector as described above is a spatial vector. Vectors are also used to store colors (red, green, blue
), angles (pan, tilt, roll)
or positions (which are basically direction vectors that start at the origin).
Addition of vectors is done by adding the corresponding components of each vector. Example:
A = [3, 1]
B = [0, 2]
A + B = [3 + 0, 1 + 2] = [3, 3]
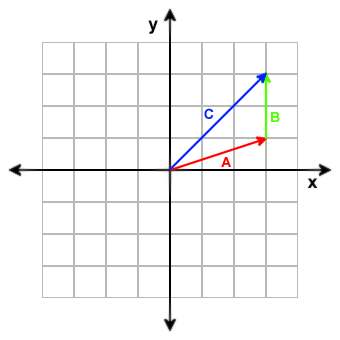
Adding two vectors results in a third vector encompassing both displacements.
Subtraction of vectors is done by subtracting the corresponding components of each vector. Example:
A = [-3, 2]
B = [2, 3]
A B = [(-3) - 2, 2 - 3)] = [-5, -1]
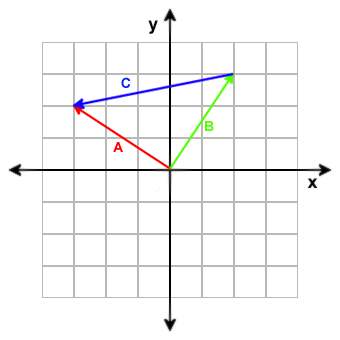
Subtracting two vectors results in a third vector pointing from the end point of the second vector to the end point of the first vector. It is often used in shaders for getting a direction vector between two points.
Multiplication of two vectors is done by multiplying the corresponding components. Example:
A = [3, 5, 1]
B = [2, 2, 3]
A * B = [3 * 2, 5 * 2, 1 * 3] = [6, 10, 3]
Multiplying two vectors is rarely used in vector math, but you'll find very often the multiplication of a vector with a matrix, which we'll deal with later.
The magnitude, or length of a vector is denoted by two vertical stripes on either side of the vector: |V|. It can be calculated with Pythagoras' theorem. For those of you that don't know or forgot it:
|V| = square-root ((Vx)2 + (Vy)2 + (Vz)2)
A vector with magnitude 1 is called a unit vector (see below).
Scaling a vector is done by multiplying each component with a scalar (a number). If the scalar is negative, the direction of the vector is also inverted. Example:
A = [2, 1]
B = 2 * A = [4, 2]
C = -0.5 * A = [-1, -0.5]
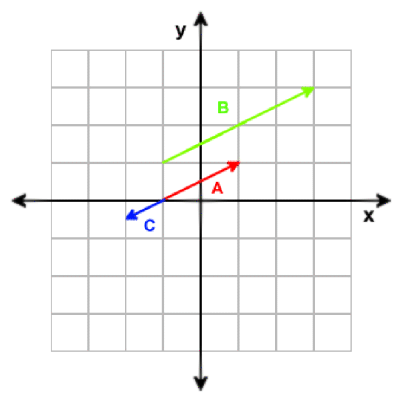
Multiplying a vector with a scalar will only change the magnitude of the vector. If the scalar is negative, the vector is also inverted.
A unit vector is any vector of length one. This does not mean that all components must be 1. Example:
A = [1, 1]
B = [0.71, 0.71]
C = [1, 0]
|A| = square-root(12 + 12) = 1.41, so A is NOT a unit vector.
|B| = square-root(0.712, 0.712) = 1, so B is a unit vector.
|C| = square-root(12, 02) = 1, so C is a unit vector.
For many calculations in lighting algorithms the vectors must be unit vectors.
For instance, normals - that are vectors perpendicular to a certain surface - are always unit vectors.
You can convert an arbitrary vector to a unit vector, this is called normalization. To normalize a vector you must divide each component of the vector by its length. Example:
V = [4, 4]
|V| = square-root(42 + 42) = square-root(32) = 5.66
Vnormalized = [4 / 5.66, 4 / 5.66] = [0.71, 0.71]
And to prove that it's actually normalized:
| Vnormalized | = square-root(0.712 + 0.712) = 1
The dot product is a very important operation in graphics programming. The interesting thing about it is that the result is not a vector but a single number (a scalar). It can be used to find the angle between two vectors. The dot product is defined as:
A · B = |A| * |B| * cos(A,B)
The dot product is the length of vector A, multiplied by the length of vector B, multiplied by the cosine of the angle between A and B. Because in shader programming we usually don't know the angle between A and B, this is of little use to us. Fortunately, there is another way to calculate the dot product:
A · B = Ax * Bx + Ay * By + Az * Bz
The dot product is the same as the sum of all vector components multiplied with each other. To find the angle between A and B, we simply divide this value by the product of |A| and |B|. In the case of normalized vectors the dot product is equal to the cosine of the angle between A and B because |A| and |B| are both 1.
The cross product of two vectors is a vector that is perpendicular to both. It is defined as:
A x B = |A| * |B| * sin(A,B) * N
where N is the unit vector perpendicular to A and B. We usually don't know the angle between A and B, but again there is another way to calculate the cross product:
A x B = [Ay * Bz - Az * By, Az * Bx - Ax * Bz, Ax * Cy - By * Bz]
In shaders, the cross product is usually used to find the third axis vector of a coordinate system when the two other vectors are known. The order of components to multiply and subtract can be memorized by the "xyzzy" rule (x component of the result = Ay * Bz - Az * By).
(Introduction and images from the Shader Workshop by Taco Cohen)
► latest version online